Recently a visitor to my site brought to my attention a white paper by Leedh processing, purporting a new “lossless” way to attenuate. https://www.processing-leedh.com/copie-de-presentation. The authors are very forthright and thorough in their claims (though they do not reveal the nature of their proprietary algorithm). However, it seems they have left out some very well-known facts.
First the claims: The designers of the attenuation algorithm (which is proprietary) claim that with a 20 dB attenuation, the results are lossless. They only give examples of 16 bit sources, so I doubt if their lossless algorithm is suitable for 24 bit sources.
They claim that dither is not needed with their proprietary algorithm, as they use special coefficients which, losslessly preserve the 16 bit data for certain values of attenuation, up to, as claimed, 30 dB. 30 dB attenuation, even 20, is more than adequate for typical processing, but 16 bit data is not typical at all, especially at 48 kHz as they illustrate. The last time I saw a 48 kHz, 16 bit music source was from a DAT machine, which have been extinct for a number of years. Also, keep in mind, that as soon as equalization or other processing is performed, the results will be greater than 16 bits and thus more than 16 bits ought to be applied to the volume control. So I wonder what the purpose or potential advantage of a 16-bit lossless volume control may be. To reiterate, 16 bit source signals are becoming rarer and rarer in practical use, not just because of digital crossovers, equalizers, and so on, but also because higher resolution sources are very available to consumers.
So, I ask, why is the designer so interested in losslessly attenuating a 16 bit source signal? For it is well known that standard attenuation via high precision calculation of both coefficient and output, coupled with proper dither — already achieves a near perfect representation of the original signal, with only dither noise added to the original signal. So I hesitate to say that this sort of calculation is “lossless” but frankly, for most purposes, we should not care about the addition of noise at a nominal -141 dBFS, which is far below the noise floor of any current DAC. Even several generations of cumulative 24 bit dither noise are fundamentally inaudible and certainly benign. Consider that for years we used analog tape with equivalent noise floors of, say, -60 dBFS, and today mastering engineers use some preamps, line amps and analog processors with as much equivalent noise as -70 or -80 dBFS, still effectively inaudible or at least considered benign.
The article states, “Figure 4 also shows how an un-dithered standard volume control introduces truncation distortion and how dithering cancels unwanted harmonics at the price of added broadband noise.” We all should agree than an undithered volume control is not acceptable but besides, the dithering noise quibble is irrelevant since no decent designer or manufacturer dithers to only 16 bits after processing: they all should dither to 24 bits to reflect the data gained by any calculation multiplication. The authors would readily admit that in any digital processor, before attenuation is applied, processes such as crossover, equalization and possibly compression or limiting are commonly applied, all of which would present a wordlength of greater than 16 bits to the volume control.
The authors wrote: “The analysis presented in Section 4 has shown that the alternative approach provides distortion-free volume control (up to a certain level of attenuation) and apparent advantages in terms of information propagation.” I’m glad that they used the word “apparent” since it is not apparent to me that lossless provides a sonic or even practical advantage given all the circumstances I describe above.
Here are some of my own measurements, which I think demonstrate that well-engineered systems already exhibit extreme signal preservation, zero distortion and inaudible noise.
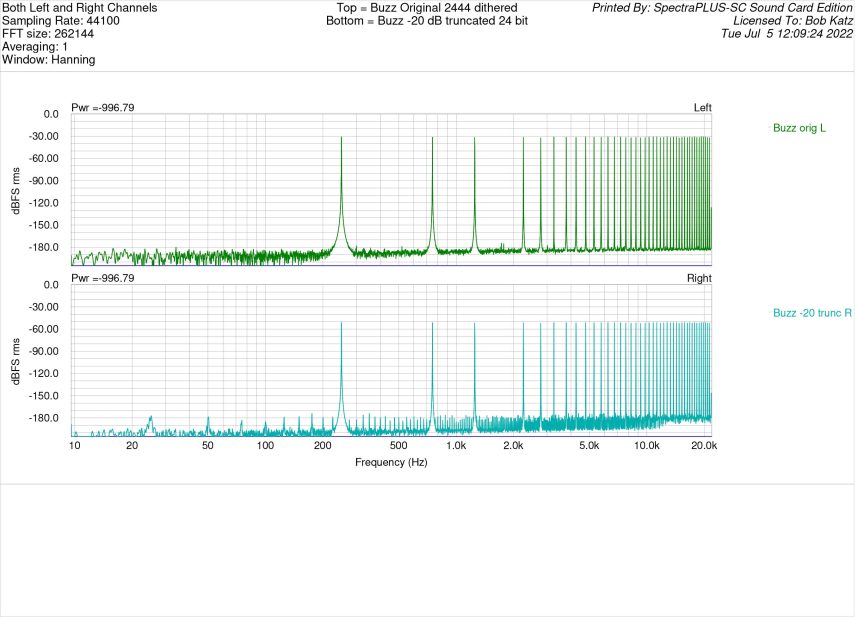
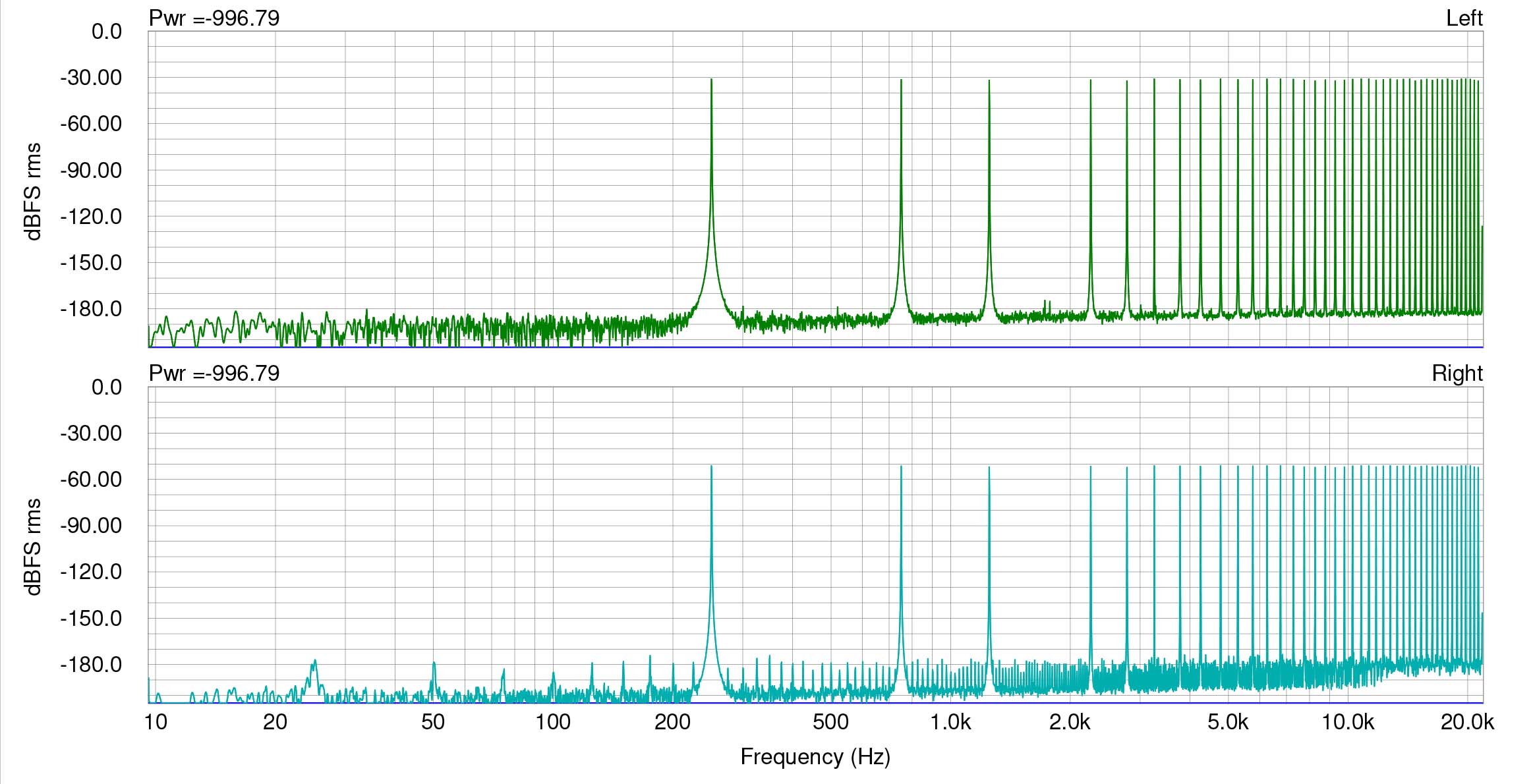
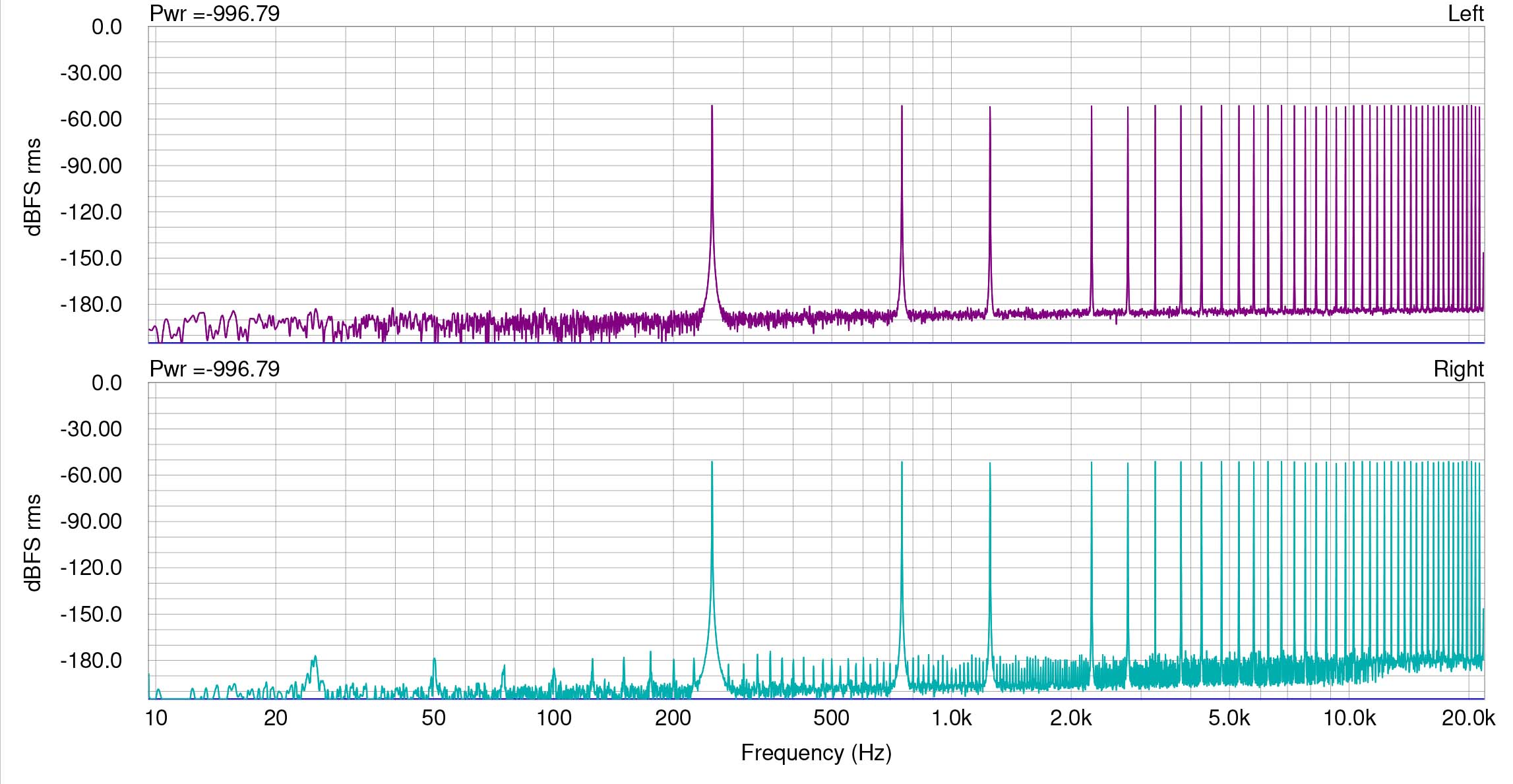
Engineer and psychoacoustician Jim Johnston has designed a very severe distortion test using multiple non-integer-related sine waves. The test has proved effective for viewing distortions from something as simple as bit truncation or as complex as that of a lossy codec. The test has a purposeful gap between 250 and 750 Hz so that any intermodulation or other distortion will easily be viewed in that section of the FFT. Spectraplus uses a 64 bit analysis engine. For this measurement I chose a high resolution FFT size of 262144 with Hanning window. For attenuation, I used Weiss Saracon, which computes in 64 bits, and for dither, Weiss’s implementation of flat 24 bit TPDF.
Here is a measurement of a 44.1 kHz buzz test signal, originally created in 64 bit float and then dithered to 24 bits. On top is an analysis of the original buzz signal, which as you can see, shows random noise between the sine wave signals, below -180 dBFS for any component. We do see two little products at around 1.6 kHz, but I did not retest to see if they are anomalies. They are almost certainly anomalies and besides, at a level of below -175 dBFS. At bottom is the same signal attenuated 20 dB in Saracon and truncated to 24 bits. Distinct and obvious distortion products can be seen from 20 to above 20 kHz.